Magnetic Moments and Spin
Nuclei of atomic number less than 45with no extra p/p- pairs
larger image
Copyright © 2009 by Phillip E. Fraley
I take a reductionist approach to physics: everything is caused by fewer mechnisms than presently used. I look everywhere for hints and ideas to that effect. In this summary, I’ve condensed 130 pages of detailed explanations into 3 pages which are the essence of my findings. My original title for a longer manuscript was “Physics From a Different Point of View.” Subjects included in the longer manuscript, but not here, are:
Bohr convinced us early in the century that there are no hidden variables. More recently, Bell’s theorem, combined with modern experiments, shows that hidden-variable interactions would be non-local and faster-than-light. No particle has been measured to interact faster-than-light; therefore, we conclude that more fundamental components, if such objects as quarks exist, cannot do so.
In this article, a new assumption about the neutron leads to different possibilities.
The neutron is the culprit and, in my opinion, the main reason we have been unable to guess about underlying nuclear structure. I think an odd neutron has two components and is a small anti-hydrogen atom not much larger than a nucleon. One component is an antiproton (p-) which is part of the nucleus and whose spin is equivalent to a proton (p) nuclear spin. The other component is a positron-like object that is in close orbit, a few femtometers radius, around the nucleus. It stays close to the antiproton. Its spin, like orbiting electrons’ spin, is not equivalent to nuclear spin. This object is hidden, and only magnetically affects the nucleus. Its energy is small, a few tens of MeVs and is detectable (other than magnetically) only through the weak interaction. The name I give to this elusive spinor is soe+, an acronym for sub-orbital positron. The soe+ also causes the isospin property.
Pairs of neutrons are proton/antiproton pairs. I’ve looked for data and reasons why combinations of soe+ and soe-, the negative counterpart of soe+, should occur near the nucleus. I have found none. However, there are plenty of reasons why both occur in high-energy particles.
Nuclear force in this schema is proton/antiproton attraction, or more fundamentally, the 5 to 4 attraction win in the total attraction and repulsion between quarks and antiquarks. The attraction and repulsion is due to spin dynamics, not charge. p is two quarks and an antiquark and p- is two antiquarks and a quark. If you count q/q- as attraction and q/q or q-/q- as repulsion, then attraction wins 5 to 4 between p and p- as stated above. The soe+ cleans up the bookkeeping. Standard-theory bookkeepers use 1/3 and 2/3 fractional charges since they haven’t guessed the soe+’s presence. Component hypotheses for muons, mesons and hyperons take a different direction also. One would not guess, for instance, that a muon is a low-energy proton-like object. That’s because there are soe+’s and soe-’s hidden in mesons and revealed in muons. There are only quarks. Up, down, and strange objects are quark, soe+, and soe- composites with various orbital and spin combinations.
Table I
Magnetic Moments and SpinNuclei of atomic number less than 45
with no extra p/p- pairs
larger image
Table I is a list of magnetic moments and spin for nucleon number < 45. Table II gives sums of columns of Table I. All of these combinations give the magnetic moment due to the orbiting soe! Column C is the deuterium cluster plus a number of alphas. Spin is one: p and p- spin 1/2’s aligned. p and p- magnetic moments cancel and only the soe+’s contribution remains. The soe+’s orbital motion is anti-aligned to the p- spin.
In A+B, the proton’s magnetic moment (B) is the surrogate for the negative of the p- magnetic moment assumed to be in A . Similarly, in A+D, the triton magnetic moment is surrogate for negative of the p- magnetic moment. In D+E, the triton magnetic moment is surrogate for its own negative magnetic moment. In B+E, the proton magnetic moment is surrogate for the negative of the triton magnetic moment. In every case, the sum leaves the soe+’s part as the result.
Soe+ magnetic moment values tend toward 0.9, 1.8 and 2.7 nuclear magnetons for j = 1/2, 3/2, and 5/2 respectively. The single value (2.7) for j = 7/2 does not fit the progression. We note all this, but have no specific model for exactly how the soe+ causes the result.
Six values for j = 1/2 and number of alphas less than three give 0.87 nuclear magnetons as an average magnetic moment for the simplest soe+ interactions. The five values for j = 1/2, number of alphas equal three (carbon cluster core), average 0.4 nuclear magnetons. Some interaction with the carbon core systematically reduces the soe+’s magnetic moment. Triton as surrogate for negative of p-, A+D, gives consistent results over the largest range of nuclear size. However, for j=3/2, these values are 0.3 nuclear magnetons less than values for deuterium cluster counterpart, C.
Table II
Columns or Sums of Columns from Table I
larger image
Neutron pairs are proton/antiproton pairs and pairs are prevalent for nucleon number A > 40. The best contrast over the largest range between nuclei with and without pairs occurs when there are multiple carbon 14’s or one pair per triple-alpha carbon cluster.
Alphas are 2 p’s and 2 n’s which become 3 p’s and 1 p- in the new schema. The binding due to alphas must be removed to obtain binding due only to p/p- pairs. Table III shows the result of assuming about 2.4 MeV for alpha-alpha bonds. Only carbon and oxygen have distinct bond counts and average 2.41 MeV per bond. Assuming bond values constant at this value, the number of bonds per alpha, plotted in Figure 1, starts to saturate at number of alphas equal 10 and has nearly zero increase after number of alphas equal fifteen where the number of bonds per alpha is 2.6. Figure 1 comes from binding energy data with zero or a few p/p- pairs in the nucleus. We then add one pair for every three alphas and estimate the difference using Figure 1. What we find is given in Table IV. For nuclear number range A = 40 to A = 84, the binding energy per pair is in the narrow range 15 to 17 MeV per pair and is maximum at 17 MeV at A = 56, the closest carbon 14 multiple to A = 52 where binding energy per nucleon is maximum.
Binding energy is divided by N, N being the number of pairs. If the sea of p’s and p-’s are evenly distributed among each other as well as among the alphas, then there are N^2 proton/antiproton bonds and N(N - 1)/2 each of p/p and p-/p- antibonds. The difference in bonds and total antibonds is proportional to N in favor of bonding.
Table III
Binding Energy Per Bond
For the Alpha Particle
Binding energy in MeV/c^2
larger image
There may be binding between p/p- pairs and alphas. If so, it’s averaged with the p/p- binding given in Table IV.
The static picture of bonds is easy to visualize, but is almost the opposite of the dynamic bonding that is actually happening. The movement of quarks and antiquarks with respect to each other is what causes mass and nuclear forces. How can this be? We look for possible ways for spin, angular momentum, mass, charge, energy, magnetic moment, and isospin to be due to one mechanism. The soe+ is an explanation for isospin, but what about the others? Spin is the best candidate to explain the rest.
Torque vector, dl/dt, has units of energy. If averaged over many local “paths” which are approximately repetitive, the magnitude, dl/dt, can be equated to mc^2 and energy. A random path on a sphere is approximately a circle. If spin h_bar follows a circle of radius r at velocity c, then dl/dt = 2*pi*h_bar*c/(2*pi*r) is the energy (mc^2). What supplies the torque that confines the spin? A spin-spin interaction with the surrounding universe. How do we do the sums with the rest of the universe? We can only make guesses. We know something about the answers.
Table IV
Binding Energy Per Bond
For for Proton-Antiproton Pairs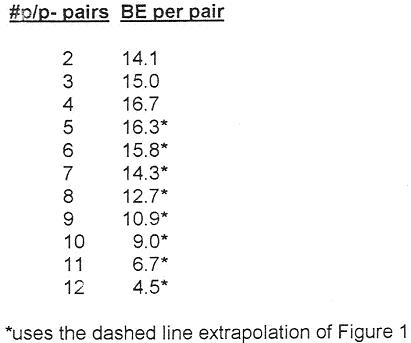
Binding energy in MeV/c^2
larger image
For a single vector being turned inward, the acceleration magnitude is v^2/r. The x-direction cosine is x/r giving (v^2/r^2)*x as one of the three vector components of acceleration. Fluctuations in near or far interactions may temporarily force the vector, either inward or outward, from the sphere defined by the average values of v and r. Terms proportional to x,y and z will bring it back.
Two spinors moving at relative velocity 2v see each other’s dl/dt magnitude as 2*h_bar*v/r'. Parameter r' is the distance between them. This equation has the same form as mass/energy above.
I used three terms proportional to x, y and z for the vector components of confinement of each of two quarks and an antiquark in a computer proton model. Additionally, three interacting vector terms for which the relative velocity could be calculated were used, two attractive and one repulsive. Random cycles occur and quarks have remained confined for as long as I’ve run the program. Figure 2 is the result for about one cycle. X and Y are plotted. Z is the radius of circles where closer quarks are larger. I did not use a hidden line algorithm so you will have to visualize that smaller circles should be behind large ones. I kept the velocity constant at 1.0 and the average radius is slightly greater than one for quarks and slightly less than one for antiquarks, giving the self-consistent result that v^2/r^2 ~ 1. A few variations on this theme have been found to be stable.
I adopted the proton model above for the proton. The antiproton is the same with quarks and antiquarks reversed. There are 21 vector terms: twelve for the p model used twice, once for the p and once for the p-, and nine smaller terms between p and p-, five attractive and four repulsive. The velocity for the two confinement centers on a circular path was varied until the acceleration was self-consistent with the dl/dt excess of attraction over repulsion. For the deuterium radius of 1.6 femtometers, this occurs at v = 0.27 c, where c is assumed to be the p and p- quark velocities. Confinement-center velocities were approximately constant for bond radii between 1 and 2 femtometers. The effect of the soe+ has been ignored for now.
Figure 1
Number of Bonds Per Alpha
versus the Number of Alphas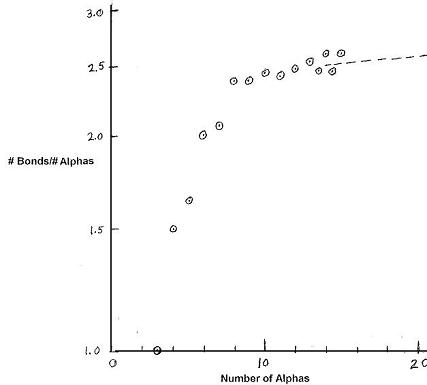
Dashed line represents the linear extrapolation
necessary to make make the p/p- binding zero for No-254
larger image
Many questions can be raised. How do you calculate mass, energy, charge, and magnetic moment? Do antiquarks go backwards in time? What is time? Why don’t p and p- annihilate each other? To list a few. I have preliminary answers for most of these and have outlined the ones for mass and energy. They are certainly colored by the new schema and calculations I’ve made thus far. However, I’ve decided not to confuse things with more models, but rather to follow up later with more explanations of my view if the sketch I’ve given here raises sufficient interest. My main purpose in writing this synopsis is to start dialogs in new directions.
The proton and nuclear bond models are parametric models with trial and error used for some parameters. The results seem reasonable. Quarks used in these models are not exactly the same as standard-theory quarks, but they are close enough to use the same word for them.
Reasons to discuss and model the innards of protons and nuclei have been given. In addition to particle properties, new meanings for missing mass, black holes, photons, neutrinos, and Bohm’s pilot waves come to mind as well. All this because of one simple guess about a hidden particle (the soe+) which leads to p/p- attraction as a major nuclear feature. We are therefore able to discuss hidden variables in terms of components and building blocks. We can devise methods for dividing problems into parts. I have divided them into parts. The soe+ model is a key which has unlocked a spectrum of possible substructures.
We have come full circle. Are these components, quarks for instance, interacting at faster-than- light speeds? I have assumed they are. dl/dt = 2*h_bar*v/r is a familiar but nevertheless strange relationship between one spinor’s perception of another’s energy, distance, relative velocity and time passage. The “perception” is instantaneous. The relative velocity (2v) is limited to 2c because that happens to be the internal velocity of quarks in protons. The impact is further limited to mostly close spinors by the 1/r form of the distance between them.
Figure 2
Quark and Antiquark Motion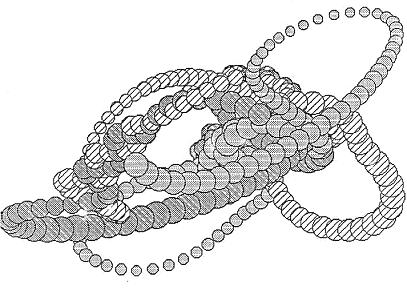
For proton model described in text.
Antiquark is the dark one.
larger image
Quantum mechanics gives the average of countless cycles and numbers of hidden variable interactions. Is it possible to derive inner detail from quantum mechanics? I don’t think so. I think we will have to work from the inside out, using simple interactions and parametric guesses to eventually calculate quantum mechanical results from more fundamental principles. I have made more than a small amount of progress, but have only empirical evidence as to the correctness of my guesses.
